Toán 10 Bài 2: Hàm số y = ax + b

1.1. Nhắc lại về hàm số bậc nhất

• Hàm số bậc nhất là hàm số được cho bằng biểu thức có dạng \(y = {\rm{ax + b}}\) với a, b là những hằng số và \({\rm{a}} \ne {\rm{0}}\).
• Hàm số bậc nhất có tập xác định là R.
• Khi \({\rm{a > 0}}\) hàm số bậc nhất \(y = {\rm{ax + b}}\) đồng biến trên R.
• Khi \({\rm{a < 0}}\) hàm số bậc nhất \(y = {\rm{ax + b}}\) nghịch biến trên R.
• Đồ thị hàm số \(y = {\rm{ax + b}}\) (\({\rm{a}} \ne {\rm{0}}\)) là một đường thẳng gọi là đường thẳng \(y = {\rm{ax + b}}\). Nó có hệ số góc là a và có các đặc điểm sau:
  • Không song song và không trùng với các trục tọa độ;
  • Cắt trục tung tại điểm B(0;b) và cắt trục hoành tại điểm \(A(\frac{{ - b}}{a};0)\)
• Cho hai đường thẳng \(y = a{\rm{x}} + b\) và hàm số \(y= a'x + b'\)
• Khi a=a' và \(b \ne b'\) thì d và d' song song với nhau.
• Khi a=a' và b=b' thì d và d' trùng nhsu.
• Khi \(a \ne a'\) thì d và d' cắt nhau.

a) Hàm số bậc nhất trên từng khoảng

• Hàm số bậc nhất trên từng khoảng là sự " lắp ghép" của nhiều hàm số bậc nhất khác nhau.

Ví dụ:

Vẽ đồ thị của hàm số  \(y = \left\{ {\begin{array}{*{20}{c}} {\frac{{ - 2}}{3}x + 5\,\,\,\,\,\,khi\,\,\,\,0 \le x \le 3}\\ {x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,\,\,3 \le x \le 6}\\ { - 2x + 18\,\,\,\,\,khi\,\,\,\,6 \le x \le 8} \end{array}} \right.\)

Hướng dẫn:

Để vẽ đồ thị hàm số này, ta vẽ đồ thị của từng hàm số tạo thành chẳng hạn:

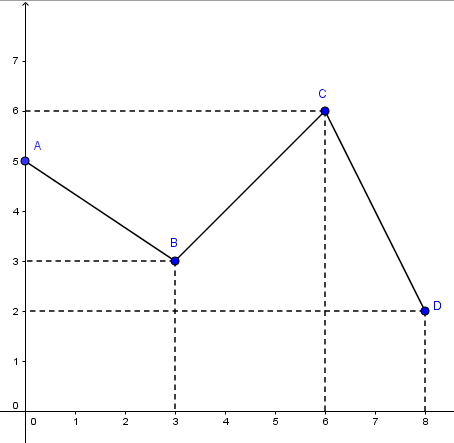
AB là phần đồ thị của \(y = \frac{{ - 2}}{3}x + 5\) ứng với \({0 \le x \le 3}\) .

BC là phần đồ thị của \(y = x\) ứng với \({3 \le x \le 6}\) .

CD là phần đồ thị của \(y = - 2x + 18\) ứng với \({6 \le x \le 8}\) .  

Ghép các phần trên lại ta được đồ thị của hàm số đã cho như hình vẽ:

b) Hàm số dạng \(y = \left| {ax + b} \right|\)

Hàm số dạng \(y = \left| {ax + b} \right|\) thực chất cũng là một dạng hàm số bậc thất trên từng khoảng.

Chẳng hạn như khi xét hàm số \(y = \left| {3x - 9} \right|\) thì theo định nghĩa trị tuyệt đối thì ta có:

• Nếu \(3x - 9 \ge 0\) tức là \(x \ge 3\) ,thì \(\left| {3x - 9} \right| = 3x - 9\) 
• Nếu \(3x - 9 < 0\) tức là \(x < 3\) ,thì \(\left| {3x - 9} \right| = 9 - 3x\)

Do đó hàm số \(y = \left| {3x - 9} \right|\) có thể viết là \(y = \left\{ {\begin{array}{*{20}{c}} {3x - 9\,\,\,\,\,\,khi\,\,\,x \ge 3}\\ {9 - 3x\,\,\,\,\,\,khi\,\,\,x < 3} \end{array}} \right.\) 

Chú ý:

Một cách khá đơn giản để vẽ đồ thị của hàm số \(y = \left| {ax + b} \right|\) là ta có thể vẽ  các đường thẳng ax+b và -ax-b rồi xóa đi phần nằm dưới trục hoành. 

Bài 1:

Tính a và b để đồ thị hàm số y=ax+b đi qua 2 điểm A(0;2) và B(1;3).

Hướng dẫn:

Thay tọa độ điểm A(0;2) vào hàm số y=ax+b ta được:

2 = a.0 + b ⇒ b = 2

Thay tọa độ điểm B(1;3) vào hàm số y=ax+b với b=2 ta được:

3 = a.1 + 2 ⇒ a = 1

vậy ta được a=1 và b=2

 

Bài 2:

Tính a và b để đồ thị hàm số y=ax+b đi qua điểm M(-1;3) và song song với đường thẳng y=-2x+5.

Hướng dẫn:

Vì đồ thị hàm số y=ax+b song song với đường thẳng y=-2x+5 ⇒ a=-2

Thay tọa độ điểm M(-1;3) vào hàm số y=ax+b với a=-2 ta được:

3 = (-1)(-2)+b ⇒ b=1

Vậy ta được a=-2 và b=1.

Trong bài học này, các sẽ được tìm hiểu về khái niệm hàm số cụ thể là hàm số y=ax+b và dạng đồ thị của nó và các ví dụ minh họa sẽ giúp các em dễ dàng nắm được nội dung bài học.

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 10 Chương 2 Bài 2 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Phương trình đường thẳng đi qua hai điểm A(-1 ;2) và B(3 ;1) là:

  • A. \(y = \frac{x}{4} + \frac{1}{4}\)
  • B. \(y = \frac{{ - x}}{4} + \frac{7}{4}\)
  • C. \(y = \frac{{3x}}{2} + \frac{7}{2}\)
  • D. \(y = - \frac{{3x}}{2} + \frac{1}{2}\)

• Câu 2:

  Cho hàm số y = x - |x|. Trên đồ thị của hàm số lấy hai điểm A và B hoành độ lần lượt là -2 và 1. Phương trình đường thẳng AB là:

  • A. \(y = \frac{{3x}}{4} - \frac{3}{4}\)
  • B. \(y = \frac{{4x}}{3} - \frac{4}{3}\)
  • C. \(y = \frac{{ - 3x}}{4} + \frac{3}{4}\)
  • D. \(y = - \frac{{4x}}{3} + \frac{4}{3}\)

• Câu 3:

  Đồ thị hàm số y = ax + b cắt trục hoành tại điểm x = 3 và đi qua điểm M(-2;4) với các giá trị a, b là:

  • A. a = 0,5; b = 3
  • B. a = -0,5 ; b = 3
  • C. a = -0,5 ; b = -3
  • D. a = 0,5 ; b = -3

• Câu 4:

  Không vẽ đồ thị, hãy cho biết cặp đường thẳng nào sau đây cắt nhau?

  • A. \(y = {\textstyle{1 \over {\sqrt 2 }}}x - 1;\,y = \sqrt 2 x + 3\)
  • B. \(y = {\textstyle{1 \over {\sqrt 2 }}}x;\,y = \frac{{\sqrt 2 }}{2}x - 1\)
  • C. \(y = - {\textstyle{1 \over {\sqrt 2 }}}x + 1;\,y = - \left( {\frac{{\sqrt 2 }}{2}x - 1} \right)\)
  • D. \(y = \sqrt 2 x - 1;\,y = \sqrt 2 x + 7\)

• Câu 5:

  Cho hai đường thẳng \({d_1}:y = \frac{1}{2}x + 100;\,{d_2}:y = - \frac{1}{2}x + 100\). Mệnh đề nào sau đây đúng?

  • A. Trùng nhau
  • B. cắt nhau và không vuông góc
  • C. song song với nhau.
  • D. vuông góc

Câu 6- Câu 15: Xem thêm phần trắc nghiệm để làm thử Online 

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Chương 2 Bài 2 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Đại số 10 Cơ bản và Nâng cao.

Bài tập 2.16 trang 36 SBT Toán 10

Bài tập 2.17 trang 36 SBT Toán 10

Bài tập 17 trang 51 SGK Toán 10 NC

Bài tập 18 trang 52 SGK Toán 10 NC

Bài tập 19 trang 52 SGK Toán 10 NC

Bài tập 20 trang 53 SGK Toán 10 NC

Bài tập 21 trang 53 SGK Toán 10 NC

Bài tập 22 trang 53 SGK Toán 10 NC

Bài tập 23 trang 53 SGK Toán 10 NC

Bài tập 24 trang 53 SGK Toán 10 NC

Bài tập 25 trang 54 SGK Toán 10 NC

Bài tập 26 trang 54 SGK Toán 10 NC

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.