Toán 10 Ôn tập chương 2 Hàm số bậc nhất và Bậc hai

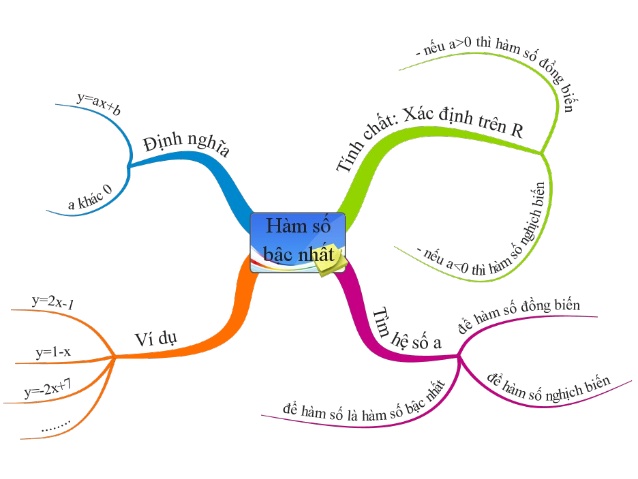
Sơ đồ tư duy hàm số bậc nhất

Khảo sát sự biến thiên và vẽ đồ thị hàm số bậc hai

Ví dụ 1:

Cho các hàm số : \(y =  - 2x + 3,\,\,y = x + 2,\,\,y = \frac{3}{2}\).

a) Vẽ đồ thị các hàm số trên.

b) Dựa vào đồ thị hãy xác định giao điểm của các đồ thị hàm số đó.

Hướng dẫn:

a) Đồ thị hàm số \(y =  - 2x + 3\) đi qua \(A\left( {0;3} \right),\,\,B\left( {\frac{3}{2};0} \right)\)

Đồ thị hàm số \(y = x + 2\) đi qua \(A'\left( {0;2} \right),\,\,B'\left( { - 2;0} \right)\)

Đồ thị hàm số \(y = \frac{3}{2}\) đi qua \(M\left( {0;\frac{3}{2}} \right)\) và song song với trục hoành.

b) Giao điểm của hai đồ thị hàm số \(y =  - 2x + 3,\,\,y = x + 2\) là \({M_1}\left( {\frac{1}{3};\frac{7}{3}} \right)\).

Giao điểm của hai đồ thị hàm số \(y =  - 2x + 3,\,\,y = \frac{3}{2}\) là \({M_2}\left( {\frac{3}{4};\frac{3}{2}} \right)\).

Giao điểm của hai đồ thị hàm số \(\,y = x + 2,\,\,y = \frac{3}{2}\) là \({M_2}\left( { - \frac{1}{2};\frac{3}{2}} \right)\).

 

Ví dụ 2:

Vẽ đồ thị hàm số \(y = 2x - 3.\) Từ đó suy ra đồ thị của:

\(\left( {{C_1}} \right):y = 2\left| x \right| - 3,\)             \(\left( {{C_2}} \right):y = \left| {2x - 3} \right|,\)       \(\left( {{C_3}} \right):y = \left| {2\left| x \right| - 3} \right|\)                                 

Hướng dẫn:

Đồ thị hàm số \(y = 2x - 3\) đi qua \(A\left( {0; - 3} \right),\,\,B\left( {2;1} \right)\) ta gọi là \(\left( C \right)\)

\(\bullet \) Khi đó đồ thị hàm số \(\left( {{C_1}} \right):y = 2\left| x \right| - 3\) là phần được xác định như sau

Ta giữ nguyên đồ thị \(\left( C \right)\) ở bên phải trục tung; lấy đối xứng đồ thị \(\left( C \right)\) ở phần bên phải trục tung qua trục tung.

\(\bullet \) \(\left( {{C_2}} \right):y = \left| {2x - 3} \right|\) là phần đồ thị \(\left( C \right)\) nằm phái trên trục hoành và đồ thị lấy đối xứng qua trục hoành của phần nằm trên trục hoành của \(\left( C \right)\).

\(\bullet \) \(\left( {{C_3}} \right):y = \left| {2\left| x \right| - 3} \right|\) là phần đồ thị \(\left( {{C_1}} \right)\) nằm phái trên trục hoành và đồ thị lấy đối xứng qua trục hoành của phần nằm trên trục hoành của \(\left( {{C_1}} \right)\).

 

Ví dụ 3:

Xác định phương trình của Parabol (P): \(y = {x^2} + bx + c\) trong các trường hợp sau:

a) (P) đi qua điểm \(A\left( {1;{\rm{ }}0} \right)\) và \(B\left( { - 2; - 6} \right)\).

b) (P) có đỉnh \(I\left( {1;{\rm{ }}4} \right)\).

c) (P) cắt trục tung tại điểm có tung độ bằng 3 và có đỉnh \(S\left( { - 2; - 1} \right)\).

Hướng dẫn:

a) Vì (P) đi qua A, B nên \(\left\{ \begin{array}{l}0 = 1 + b + c\\ - 6 = 4 - 2b + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b + c =  - 1\\2b - c = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\c =  - 4\end{array} \right.\).

Vậy (P):\(y = {x^2} + 3x--4\) .

b) Vì (P) có đỉnh \(I\left( {1;{\rm{ }}4} \right)\) nên\(\left\{ \begin{array}{l}\frac{{ - b}}{2} = 1\\ - \frac{{{b^2} - 4c}}{4} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b =  - 2\\c = 5\end{array} \right.\).

Vậy (P):\(y = {\rm{ }}{x^2}--2x + 5\) .

c) (P) cắt Oy tại điểm có tung độ bằng 3 suy ra \(c = 3\)

(P) có đỉnh \(S\left( { - 2; - 1} \right)\)suy ra: \(\left\{ \begin{array}{l} - \frac{b}{{2a}} =  - 2\\ - 1 = 4a - 2b + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4\\a = 1\end{array} \right.\)

 

Ví dụ 4:

Cho hàm số \(y = {x^2} - 6x + 8\)

a) Lập bảng biến thiên và vẽ đồ thị các hàm số trên.

b) Sử dụng đồ thị để biện luận theo tham số \(m\) số điểm chung của đường thẳng \(y = m\) và đồ thị hàm số trên.

c) Sử dụng đồ thị, hãy nêu các khoảng trên đó hàm số chỉ nhận giá trị dương.

d) Sử dụng đồ thị, hãy tìm giá trị lớn nhất, nhỏ nhất của hàm số đã cho trên \(\left[ { - 1;5} \right]\).

Hướng dẫn:

a) Ta có \( - \frac{b}{{2a}} = 3,\,\, - \frac{\Delta }{{4a}} =  - 1\)

Bảng biến thiên:

Suy ra đồ thị hàm số \(y = {x^2} + 3x + 2\) có đỉnh là \(I\left( {3; - 1} \right)\), đi qua các điểm \(A\left( {2;0} \right),\,\,B\left( {4;0} \right)\)

Nhận đường thẳng x = 3\) làm trục đối xứng và hướng bề lõm lên trên.

b) Đường thẳng \(y = m\) song song hoặc trùng với trục hoành do đó dựa vào đồ thị ta có

Với \(m <  - 1\) đường thẳng \(y = m\) và parabol \(y = {x^2} - 6x + 8\) không cắt nhau

Với \(m =  - 1\) đường thẳng \(y = m\) và parabol \(y = {x^2} - 6x + 8\) cắt nhau tại một điểm(tiếp xúc)

Với \(m >  - 1\) đường thẳng \(y = m\) và parabol \(y = {x^2} - 6x + 8\) cắt nhau tại hai điểm phân biệt

c) Hàm số nhận giá trị dương ứng với phần đồ thị nằm hoàn toàn trên trục hoành

Do đó hàm số chỉ nhận giá trị dương khi và chỉ khi \(x \in \left( { - \infty ;2} \right) \cup \left( {4; + \infty } \right)\).

d) Ta có \(y\left( { - 1} \right) = 15,\,\,y\left( 5 \right) = 13,\,\,y\left( 3 \right) =  - 1\), kết hợp với đồ thị hàm số suy ra

\(\mathop {\max }\limits_{\left[ { - 1;5} \right]} y = 15\)  khi và chỉ khi\(x =  - 1\)

\(\mathop {\min }\limits_{\left[ { - 1;5} \right]} y =  - 1\) khi và chỉ khi \(x = 3\)

Nội dung bài giảng sẽ giúp các em tổng hợp kiến thức về các hàm số đã được học gồm hàm số y=ax+b và hàm số bậc hai thông qua các sơ đồ. Bên cạnh đó các em còn được ôn lại phương pháp giải toán thông qua một số bài tập có hướng dẫn giải chi tiết.

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 10 Ôn tập chương II để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ:

  

  Kết luận nào trong các kết luận sau là đúng:

  • A. Đồng biến trên \(\mathbb{R}\)
  • B. Hàm số chẵn.
  • C. Hàm số lẻ  
  • D. Cả ba đáp án đếu sai

• Câu 2:

  Với những giá trị nào của m thì hàm số \(y =  - {x^3} + 3\left( {{m^2} - 1} \right){x^2} + 3x\) là hàm số lẻ:

  • A. \(m = 1\)
  • B. \(m =  - 1\)
  • C. \(m =  \pm 1\)
  • D. một kết quả khác.

• Câu 3:

  Cho đồ thị hàm số \(y = ax + b\) như hình vẽ:

  

  Khi đó giá trị a, b của hàm số trên là:

  • A. \(a = 3;b =  - 3\)
  • B. \(a =  - 1;b = 3\)
  • C. \(a = 3;b = 3\)
  • D. \(a = 1;b =  - 3\)

• Câu 4:

  Khẳng định nào về hàm số \(y = 3x + 5\) là sai:

  • A. Đồ thị cắt Oy tại \(\left( {0;5} \right)\)
  • B. Nghịch biến R   
  • C. Đồ thị cắt Ox tại \(\left( { - \frac{5}{3};0} \right)\)
  • D. Đồng biến trên R

• Câu 5:

  Trong các đồ thị hàm số có hình vẽ dưới đây, đồ thị nào là đồ thị hàm số \(y =  - {x^2} + 4x - 3\)

  

  • A. Hình 2
  • B. Hình 3
  • C. Hình 1
  • D. Hình 4

• Câu 6:

  Trong các hàm số sau, hàm số nào có đồ thị  đi qua điểm \(M\left( {1;3} \right)\) và trục đối xứng \(x = 3\):

  • A. \(y =  - {x^2} + 6x\)
  • B. \(y = {x^2} + 3x - 1\)
  • C. \(y = {x^2} + 2x - 2\)
  • D. \(y =  - {x^2} + 6x - 2\)

• Câu 7:

  Đồ thị hàm số \(y = {m^2}x + m + 1\)  tạo với các trục tam giác cân khi m bằng:

  • A. 1
  • B. \( - 1\)
  • C. \( \pm 1\)
  • D. 0

Câu 8- Câu 20: Xem thêm phần trắc nghiệm để làm thử Online 

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Ôn tập chương II sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Đại số 10 Cơ bản và Nâng cao.

Bài tập 6 trang 50 SGK Đại số 10

Bài tập 7 trang 50 SGK Đại số 10

Bài tập 8 trang 50 SGK Đại số 10

Bài tập 10 trang 51 SGK Đại số 10

Bài tập 39 trang 63 SGK Toán 10 NC

Bài tập 40 trang 63 SGK Toán 10 NC

Bài tập 41 trang 63 SGK Toán 10 NC

Bài tập 42 trang 63 SGK Toán 10 NC

Bài tập 43 trang 63 SGK Toán 10 NC

Bài tập 44 trang 64 SGK Toán 10 NC

Bài tập 45 trang 64 SGK Toán 10 NC

Bài tập 46 trang 64 SGK Toán 10 NC

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.