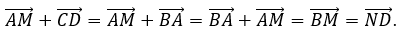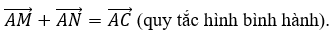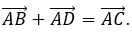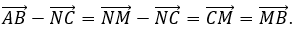Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD.
Câu hỏi :
Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Cặp vectơ nào trong số các cặp vectơ sau đây không bằng nhau?
A. \(\overrightarrow {NC} + \overrightarrow {MC} \) và \(\overrightarrow {AD} \)
B. \(\overrightarrow {AM} + \overrightarrow {CD} \) và \(\overrightarrow {ND} \)
C. \(\overrightarrow {AB} - \overrightarrow {NC} \) và \(\overrightarrow {MB} \)
D. \(\overrightarrow {AM} + \overrightarrow {AN} \) và \(\overrightarrow {AB} + \overrightarrow {AD} \)
* Đáp án
A
* Hướng dẫn giải
Vì \(\overrightarrow {MC} = \overrightarrow {AN} \)
Ta có \(\overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {AN} = \overrightarrow {AN} + \overrightarrow {NC} = \overrightarrow {AC} \ne \overrightarrow {AD} \)
Chọn A.
Lưu ý: Trong phương án B, vì CD→=BA→, ta có
Trong phương án D, vì tứ giác AMCN là hình bình hành nên ta có:
Vì tứ giác ABCD là hình bình hành nên
Suy ra
Trong phương án C,
Chọn A.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Hình học 10 Bài 2 Tổng và hiệu của hai vectơ
Copyright © 2021 HOCTAP247

.PNG)